Логарифмом додатного числа b з основою a (a>0, a≠1) називається показник степеня, до якого треба піднести a, щоб отримати b.
Основна логарифмічна тотожність
Означення логарифма можна коротко записати так:
Ця рівність справедлива при b>0, a>0, a≠0 і називається основною логарифмічною тотожністю.
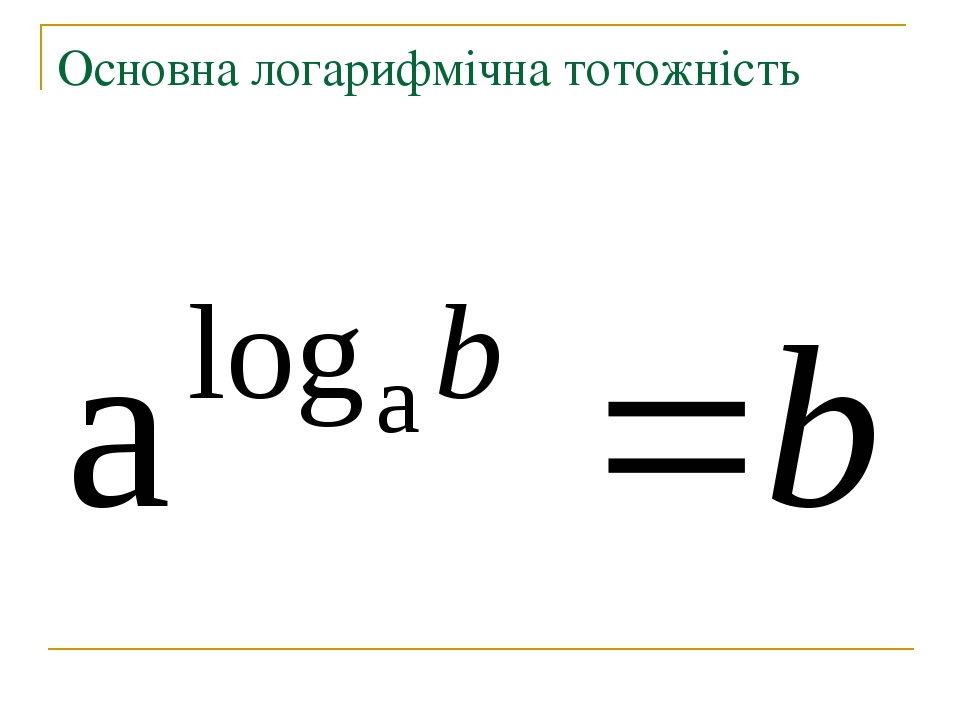
Які арифметичні дії дозволяє замінити використання логарифмів?
ВідповістиВидалитиВикористання логарифмів дозволяє замінити множення, ділення, піднесення до степеню та видобування кореня на більш прості операції множення - додавання, ділення - віднімання, піднесення до степеню - множення на показник степеню числа, видобування кореня -ділення на показник кореня числа.
ВидалитиЧи є щось спільне в логарифмів з похідною?
ВідповістиВидалитиЛогарифми тісно взаємопов'язані з похідною, адже саме метод логарифмічного диференціювання стає в нагоді при дифренціюванні добутку кількох функцій або їх частки. Його зручно застосовувати при дифенеціюванні виразів, що містять корені із дробів (функцій), а також коли показник функції також являє собою складену функцію y=f(x)g(x). Похідну від логарифма функції називають логарифмічною похідною.
ВидалитиЧи справедливе логарифмічна тотожність при b<o?
ВідповістиВидалитиЛогарифмічна тотожність при b<0, не буде справедливою, оскільки всі її елементи повинні бути додатніми.
Видалити